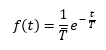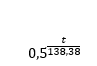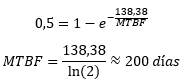El examen de física para el acceso a la universidad (EVAU) de este año en Madrid contenía una pregunta sobre la descomposición atómica.

La dificultad podía estribar no tanto en conceptos físicos como estadísticos. Una ecuación tan simple y aparentemente inocente como la exponencial: 

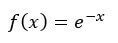
contiene mucha información y modela fenómenos a veces poco intuitivos.

La función exponencial representa la probabilidad de sucesos aleatorios que no tienen memoria, es decir, que no se vuelven más probables cuando llevan mucho tiempo sin haber sucedido. Si sabemos que un autobús pasa cada diez minutos y llevamos nueve esperando en la marquesina, en esos momentos su llegada es mucho más probable que si acabásemos de llegar a la parada. Por el contrario, aunque un dado en promedio saca el 6 una de cada seis veces, no porque llevemos cinco veces sin sacarlo hay más probabilidades de que vaya a salir la próxima vez: sino que estamos como al principio. Sin embargo, el autobús sí tiene memoria y no estamos como al principio.

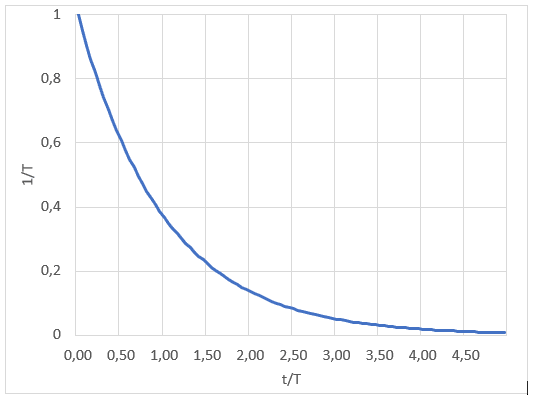
Se ha observado que los equipos electrónicos, y los componentes con los que se construyen, sufren fallos aleatorios que no tienen que ver con el envejecimiento del material (es decir, que no tienen memoria) sino que siguen una función de densidad de probabilidad exponencial:

Si aplicamos la definición de «media» a la ecuación anterior obtenemos el valor de ‘T’: es el tiempo medio que tarda en fallar un componente y cual debemos conocer para averiguar la probabilidad de fallo en un periodo de tiempo.

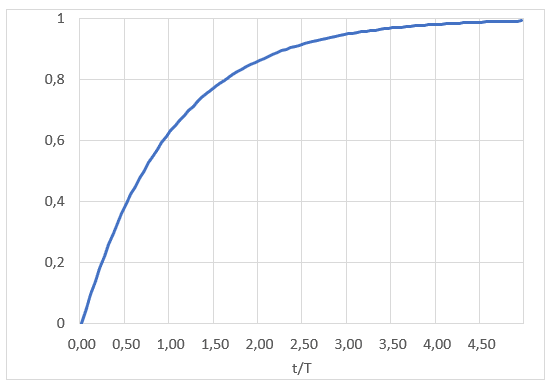
La integral de la función de densidad representa la probabilidad de que un suceso haya ocurrido hasta un determinado momento ‘t’ y se llama función de distribución:

Los fabricantes caracterizan este fenómeno con el parámetro MTBF (mean time between failures), cuyo valor colocaríamos en el lugar de ‘T’ en la ecuación anterior. Someten miles de piezas a ensayos de envejecimiento y encuentran que, en promedio, fallan en ese tiempo. Pero la probabilidad de que un componente falle cuando alcanza su vida media no es, como podríamos inicialmente pensar, de un 50%. Si sustituimos ‘t’ por ‘T’ en la ecuación anterior encontramos que la probabilidad acumulada hasta ese momento es:

No es raro que un equipo electrónico tenga un MTBF de medio millón de horas. Eso son 57 años, lo que puede llevar a pensar que no necesitamos que sea tan fiable si se quedará obsoleto mucho antes. Pero el MTBF no es la vida útil. Por lo tanto, siempre interesa tener un MTBF elevado porque implica que, de cada 57 equipos que tengamos instalados, desde el primer día va a fallar uno de media anual. De tal forma, si necesitamos que ese parque funcione durante diez años, mejor guardémonos al menos diez equipos de repuesta en el almacén.

Un isótopo radiactivo se comporta estadísticamente igual que un aparato electrónico. En la EVAU planteaban un problema con Polonio 210, con un periodo de semidesintegración de 138,38 días. Esto significa que una cantidad inicial de ese elemento se reduce a la mitad cada vez que transcurre ese plazo, proporcionalmente al factor:

Pero, ¿cuál es el equivalente del MTBF de un átomo de Polonio 210? ¿Cuánto tiempo tarda en desintegrarse un átomo, en promedio, cuando observas muchos? En el ámbito de la física se denomina “vida media” y lo podemos calcular fácilmente a partir del periodo de semidesintegración:

Si dudabas que estudiar física en bachillerato pudiera servir para algo, has podido comprobar que la comprensión de la naturaleza y su modelización matemática pueden tener aplicaciones inesperadas.

En Teldat calculamos el MTBF de nuestros equipos de telecomunicaciones a partir de los parámetros de los componentes electrónicos que los conforman. Tan importante es que el hardware sea fiable como conocer el valor de esa fiabilidad para poder hacer estimaciones de reparaciones y disponibilidad de servicio.